“Revolutionizing Anti-Corrosion: Harnessing Native Strain in Ru-Enhanced Co3O4 for Superior Acidic Oxygen Evolution”

Chemical Compounds

Cobalt(II) nitratehexahydrate (Co(NO₃)₂·6H₂O, 99%, Thermo Scientific), 2-methylimidazole (2-MIM, 99%, Thermo Scientific), Cetyltrimethylammonium bromide (CTAB, 99%, Shanghai Maclin Biochemical Expertise Co., Ltd), Tannic acid (ACS reagent, Sigma-Aldrich), Ruthenium (III) chloride hydrate (ACS reagent, AIKE REAGENT), Perchloric acid (HClO₄, 70%, Sigma-Aldrich), Ethanol (C₂H₅OH, absolute, VWR Chemical substances BDH), 2-propanol (C₃H₈O, HPLC grade, VWR Chemical substances BDH).

You might also like

Ride the Back-to-School Surge: Student Innovators Shaping the Future of Water Energy!

April 7, 2025

Lessons from Across the Atlantic: Insights from Two European Utilities for the U.S.

April 10, 2025

Preparation of ZIF-67 Nanocubes (NCs)

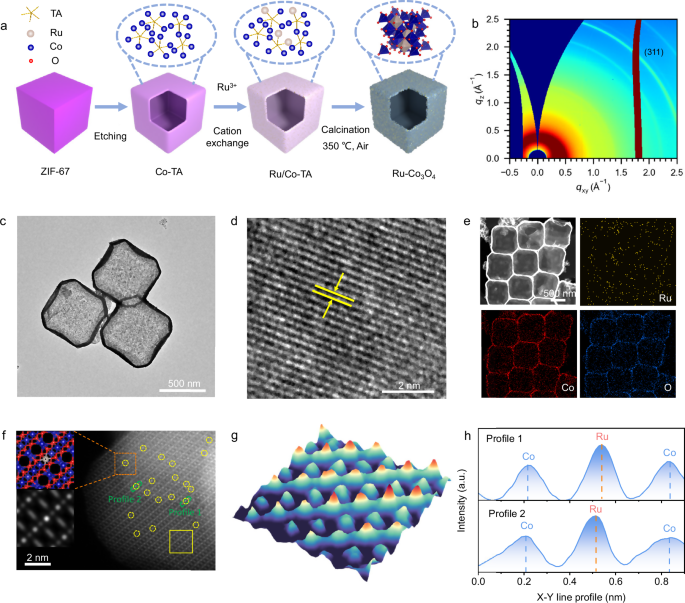
ZIF-67 NCs were synthesized utilizing a methodology previously described³⁰. Specifically, 292 mg of Co(NO₃)₂•6H₂O was dissolved in 10 mL of deionized water with the addition of 4 mg of CTAB. Afterward, the mixture was swiftly introduced into 70 mL of an aqueous solution containing 4.54 g of 2-MIM and stirred for 40 minutes at room temperature. The final product was gathered through centrifugation and thoroughly rinsed multiple times with ethanol.

Preparation of Co-tannic Acid Complex Nanoboxes (Co-TA NBs)

Initially, 60 mg of ZIF-67 nanocubes (NCs) were dispersed in 20 mL of ethanol before being transferred into a solvent mixture comprising 300 mL of ethanol and DI water in a 1:1 volume ratio containing 1 mg mL^-1 of tannic acid (TA). The resultant mixture was stirred at room temperature for 10 minutes. Following this, the product was isolated through centrifugation and subjected to several ethanol washes. Finally, the product was dried in an oven at 60 °C.

Preparation of Co₃O₄ NBs

The Co-TA nanoboxes underwent annealing at 350 °C for 3 hours, with the temperature increasing at a rate of 1 °C per minute in an air atmosphere, followed by natural cooling to ambient temperature.

Preparation of Ru-Co₃O₄ NBs

50 mg of Co-TA NBs was dissolved in 10 mL of ethanol. Following this, 4 mL DI water containing 10 mM RuCl₃•xH₂O was added dropwise to the prepared dispersion, which was then stirred at room temperature for 3 h. The resulting product was collected via centrifugation, washed several times with ethanol, and ultimately dried in an oven at 70 °C. The obtained powder was placed in a tube furnace and heated at 350 °C for 3 h with a heating rate of 1 °C min⁻¹ in an air environment.

Material Characterizations

X-ray diffraction (XRD) patterns were recorded over the range of 5° to 90° 2θ using a Bruker D8 Advance X-ray diffractometer, operating at a scan rate of 3° per minute. The apparatus was equipped with Cu Kα radiation (λ = 1.5406 Å) and a beryllium window. The structures and morphologies of the materials were characterized by TEM (Titan Themis Z). HRTEM and elemental mapping were conducted using the Titan Cs Probe instrument. Microstructural and morphological assessments were performed via scanning electron microscopy (SEM, Quattro FEG, FEI Ltd, CZ). The samples underwent wet digestion and analysis via an Agilent 5110 ICP-OES. XPS data were collected using ESCALAB 250 xi. The wide-angle X-ray scattering (WAXS) measurements were conducted at the Beijing Synchrotron Radiation Facility (BSRF), 1W1A beamline, utilizing X-ray with a wavelength of 1.54 Å. Characterization results of Ru-Co₃O₄ samples shown in Figs. 1 and 2 are based on the sample with a Ru content of 4.49 wt%.

X-ray Absorption Fine Structure Experiments

XAFS spectra were gathered in fluorescence mode at the 1W1B beamline of the BSRF, employing a double crystal Silicon (111) monochromator to adjust photon energy with an average energy resolution ΔE/E of 1-3 × 10⁻⁴ @ 9 keV. The electron storage ring functioned at an energy level of 2.5 GeV with a current range of 200 mA. The beam intensity was measured utilizing an ionization chamber filled with 100% N₂ for Co K-edge detection and 100% Ar for Ru K-edge detection. A Lytel detector filled with 100% Ar was employed to record the fluorescence signal. Co and Ru foil spectra were obtained in transmission mode to serve as a reference for energy calibration. XANES and EXAFS were utilized to investigate the valence states, coordination environments, and structural disorder within the samples. The data analysis was conducted utilizing the ATHENA and ARTEMIS modules (version 0.9.26) within the IFEFFIT software suite⁶². EXAFS functions underwent Fourier transformation into R space, using a k-weight of two in the ranges of 2.98–11.83 Å⁻¹ for the Co edge and 2.78–10.79 Å⁻¹ for the Ru edge with a hanning window (dk = 1.0 Å⁻¹). For the absorption edges of Co and Ru, the amplitude reduction factors (S₀²) were found to be 0.7 and 0.72, respectively, through separate fittings of Co and Ru foil XAFS data. Fittings were continuously performed in R space with a k-weight of two. For the EXAFS data processing, this research focuses on the Co-O coordination shells of interest: Co_Td-O, Co_Oh-O, Co_Oh-Co_Oh, and Co_Td-Co_Oh, within distance ranges of 1.81–3.35 Å. Considering factors such as signal-to-noise ratio, data quality, and the physical characteristics of the system, we determined that the R-space range (1.15–3.45 Å) is the most suitable for EXAFS fitting. The Ru K-edge XANES spectra were simulated using full multiple scattering (FMS) and the finite difference method (FDM) by solving the Schrödinger equation. Theoretical XANES calculations at the Ru K-edge were conducted using the FDMNES code, employing the real-space FMS scheme and the Muffin-tin approximation for the potential⁶³. To simulate the XANES features, calculations were performed including all atoms within 6.0 Å from the central Ru atom and solely the transition electric dipolar components were calculated. The calculations utilized energy steps of 0.5, 0.2, 0.5, 1.0, and 2.0 eV corresponding to the energy ranges of [−200.0, −2.0], [−2.0, 3.0], [3.0, 10.0], [10.0, 20.0], and [20.0, 300.0], respectively. The calculated outcomes were convoluted using an arctangent function to obtain the final spectrum. Soft XAS data for the O K-edge were gathered in total electron yield (TEY) mode at beamline 4B7B of the BSRF. The storage ring functioned at an energy of 2.5 GeV with a maximum electron current of 250 mA. The energy step sizes employed during data collection were 0.5 eV, 0.05 eV, 0.1 eV, 0.2 eV, and 0.3 eV for the energy ranges of [−33.1, −19.1] eV, [−19.1, −14.6] eV, [−14.6, −2.5] eV, [−2.5, 1.3] eV, and [1.3, 28.0] eV, respectively.

Operando XAFS Experiments

The in situ Ru and Co K-edge spectra of the catalyst were obtained utilizing an in situ reaction cell filled with 0.1 M HClO₄ electrolyte. The powdered sample was prepared as a homogeneous catalyst ink at a concentration of 5 mg/mL and applied to a 1 × 1 cm² carbon paper to achieve a catalyst loading of 1 mg/cm². The carbon paper with the catalyst was then placed into the in situ reaction cell and sealed using Kapton film. To examine the evolution of the active site during the electrochemical reaction, a range of representative

potentials (1.03–1.63 V) was applied to the electrode. Each spectrum was recorded three times in succession using rapid-scanning XAFS techniques to ensure reliable signal-to-noise XAFS data. During the data collection process for the Co K-edge, the following energy steps were used for their respective energy ranges: 4.0 eV for [−200, −20] eV, 1.0 eV for [−20, −10] eV, 0.5 eV for [−10, 50] eV, 1.0 eV for [50, 150] eV, 2.0 eV for [150, 300] eV, 3.0 eV for [300, 600] eV, and 4.0 eV for [600, 740] eV. Similarly, for the Ru K-edge, the energy steps employed were 4.0, 1.5, 2.0, 2.0, 3.0, and 4.0 eV for the energy ranges of [−240, −20], [−20, 50], [50, 200], [200, 300], [300, 600], and [600, 740], respectively.

Electrochemical measurements

The electrochemical performance of the samples for the OER was assessed using a standard three-electrode setup in a 0.1 M HClO₄ electrolyte at room temperature. A 0.1 M HClO₄ electrolyte solution (pH = 1) was prepared by diluting 70% HClO₄ in deionized water at ambient temperature. The solution was continuously stirred for 30 minutes to ensure a uniform solution was formed. The Hg/Hg₂SO₄ reference electrode used in electrochemical assessments required calibration. Specifically, the calibration was performed in a hydrogen-saturated, high-purity 0.1 M HClO₄ electrolyte, using a Pt wire as the working electrode, Hg/Hg₂SO₄ as the reference electrode, and another Pt wire as the counter electrode. Cyclic voltammograms (CVs) were recorded at a scan rate of 1 mV s⁻¹, with the thermodynamic potential for the hydrogen electrode reactions determined from the point at which the current crossed zero (Supplementary Fig. 17a, b). To prepare the catalyst ink, 5.0 mg of the catalysts was dispersed in a mixed solution consisting of 0.50 mL deionized water, 0.48 mL isopropanol, and 0.02 mL of a 5 wt% Nafion solution. The mixture was then subjected to ultrasonication for at least 30 minutes to ensure the formation of a homogeneous ink. The catalyst ink was applied onto 0.5 × 0.5 cm² carbon paper to achieve a catalyst loading of 0.7 mg cm⁻². A platinum sheet electrode clamp was utilized to secure carbon fiber papers loaded with catalysts. Measurements were conducted on a CHI 760E electrochemistry workstation. The setup included a carbon rod as the counter electrode and a Hg/Hg₂SO₄ electrode as the reference electrode, while the carbon fiber papers impregnated with catalysts acted as the working electrode. The Nernst equation (left({E}_{{{{rm{RHE}}}}}={E}_{{{{rm{Hg}}}}/{{{{rm{Hg}}}}}_{2}{{{{rm{SO}}}}}_{4}}+0.0591times {{{rm{pH}}}}+0.656right)) was employed to adjust all potentials against a reversible hydrogen electrode (RHE). Notably, linear sweep voltammetry (LSV) at a scan rate of 5 mV s⁻¹ was employed to evaluate the catalysts’ electrochemical activity towards the OER. The overpotential (η) for the OER at a current density of 10 mA cm⁻² was calculated using the equation η = E_RHE – 1.23 V. Furthermore, the Tafel slope was derived using the Tafel equation, expressed as η = b log j + a. In this equation, η denotes the overpotential related to the OER, j signifies the current density, and b represents the Tafel slope. To analyze the electrochemical characteristics, Electrochemical impedance spectroscopy (EIS) was executed at a designated potential, employing a ten mV amplitude over a frequency range from 0.1 Hz to 100 kHz. An iR compensation of 90% was applied to all polarization curves unless stated otherwise. The uncompensated resistance (R) was determined through electrochemical impedance spectroscopy. The resistance values found were 11.85 Ω for Co₃O₄, 13.24 Ω for RuO₂, 11.95 Ω for Ru-Co₃O₄ (1.33 wt%), 12.03 Ω for Ru-Co₃O₄ (3.21 wt%), 11.89 Ω for Ru-Co₃O₄ (4.49 wt%), 11.94 Ω for Ru-Co₃O₄ (7.06 wt%), and 11.50 Ω for Ru-Co₃O₄ (8.67 wt%). The electrochemically active surface area (ECSA) of the catalysts was estimated from the electrochemical double-layer capacitance (C_dl) of the catalytic surface using the following equation:

where C_dl was derived from the CVs that were dependent on the scan rate, recorded in the non-Faradaic region between 0.81 and 0.91 V vs. RHE in 0.1 M HClO₄, utilizing scan rates of 10, 20, 30, and 50 mV s⁻¹. In this context, S denotes the actual surface area of the smooth metal electrode, which typically corresponds to the geometric area of the glassy carbon electrode, where S = 0.28 cm². The specific capacitance (C_s) for a flat surface generally varies between 20 and 60 μF cm⁻². In this study, a C_s value of 40 μF cm⁻² was employed to estimate the ECSA.

Molecular simulations

The standard parameters used during ab initio molecular dynamics (AIMD) in CP2K/Quickstep^64,65 utilizing the hybrid Gaussian plane wave method are established as follows: The PBE functional⁶⁶ is utilized to describe the exchange-correlation interactions, supplemented by a DFT-D⁶⁷ correction to accommodate dispersion effects. The remaining core electrons were represented by Goedecker-Teter-Hutter (GTH) pseudo-potentials⁶⁸. The plane wave cutoff was 400 Ry with a double-zeta DZVP basis set. The time step was established at 0.5 fs maintained at 300 K by employing the canonical ensemble (NVT) with the Nosé-Hoover thermostat during AIMD. Well-tempered AIMD⁶⁹ simulations were conducted to accelerate the sampling of configuration space and explore the reaction landscape as the coordination number changes, combined with the PLUMED plugin⁷⁰. The bias term is defined as a sum of Gaussian hills with height h and width ω:

Here, the bias factor was set to 100. Gaussian hills of 0.3 width and 3.3 kJ mol⁻¹ initial height were applied in a two-dimensional set of collective variables, defined by coordination numbers (CN). The selected collective variables are based on coordination numbers. To describe the coordination of cobalt oxide Co_j with a set of oxygens, CN is defined by:

r_ij – inter-atomic distance between atom i and atom j,

d₀ – the Co-O equilibrium distance,

r₀ – the acceptance distance of the switching function, which, coupled with the n/m ratio, controls at which distance the O atom is not considered as bonded.to Co.

n, m – two whole exponents where n < m.

In this investigation, a ratio of 9/14 (n = 9, m = 14), a Co-O equilibrium distance of 1.5 Å, and a r₀ of 0.9 Å have been selected. Two combined variables are established as follows: The variable CN_W denotes the coordination diversity of examined Co atoms with water oxygen molecules and excess chloric acid oxygen atoms. CN_L signifies the coordination diversity of investigated Co atoms with the oxygen atoms associated with the structural framework of Co₃O₄. The error associated with this procedure is below 2 kJ mol⁻¹. The AIMD configurations derived from trajectories are included in Supplementary Information 1.

DFT computing specifics

All theoretical assessments were conducted utilizing the Vienna ab initio software package (VASP 5.4.4)⁷¹. DFT models employed for theoretical analyses are formulated by taking into account the subsequent factors: 1) The elemental composition of metals in the model is determined by evaluating the actual composition of catalysts. 2) XRD, XANES, and EXAFS techniques can offer crucial structural data of materials, which are very beneficial for creating DFT models. For instance, the WT k-R maps provided local structural information, assisting in the identification of the single atom arrangement. A least-squares EXAFS fitting was further performed to reveal quantitative structural parameters of Ru in Ru-Co₃O₄. Additionally, a simulated XANES spectrum that closely aligned with experimental data regarding energy placement and spectral intensity for incorporates a, b, c, and d (Fig. 2e), bolstering the conclusion that Ru species in Ru-Co₃O₄ primarily occupy octahedral (Oh) sites coordinated with lattice oxygen, which corresponds well with EXAFS fitting results. This strongly suggests that the structure of Ru-Co₃O₄ is in the form of Ru single atom. The projector augmented-wave method was applied to manage core electrons with default potentials, while the Perdew-Burke-Ernzerhof (PBE) GGA exchange-correlation functional was employed with spin polarization⁶⁶. The self-consistent field (SCF) iterations were set to converge at a criterion of 10⁻⁶eV per unit cell. The ENCUT parameter, which dictates the size of the basis set, was kept at 450 eV. For slab computations, the k-point grid was sampled using a 3 × 3 × 1 Monkhorst-Pack grid⁷², whereas a 12 × 12 × 12 grid was utilized for bulk calculations. Core electrons were treated through the projector-augmented wave (PAW) methodology. Geometry optimization convergence was achieved when forces reached 0.01 eV Å⁻¹.

Adsorption energies (∆E_adverts) describe the energetic characteristics of attached molecules on surfaces and are defined as:

where E_adverts/sub is the total energy of the optimized structure with adsorbed species, E_sub is the total energy of the optimized bare surface structure, and E_mol is the total energy of the adsorbed gas species.

The differential Gibbs free energies of adsorption (∆G_adverts) were derived based on DFT total energies, with adjustments made for entropy change (T∆S, where T represents temperature and S signifies entropy) and for the difference in vibrational energy (∆E_vib) and zero-point energy (∆E_ZPE), both obtained from vibrational frequencies:

The optimized structural models are provided in Supplementary Information 1.