Revolutionizing Hydro-Turbine Fault Prognosis: Unleashing the Power of IWSO-Enhanced CNN-LSTM Neural Networks!

Enhanced wavelet threshold technique

Primarily grounded in wavelet transformation concepts, the WT algorithm accurately retrieves significant indicators by utilizing crucial discrepancies between authentic indicators and noise indicators within wavelet coefficients ⁴⁴. This algorithm, noted for its excellent efficacy, finds widespread application across various domains, particularly in signal noise reduction and feature extraction ^45,46.

The fundamental principle of the WT algorithm is the capability of wavelet transformation to break down a signal into wavelet coefficients across diverse frequencies and scales. Valuable and noisy signals typically exhibit markedly different behaviors in relation to these coefficients. By selecting a suitable threshold value, the wavelet thresholding algorithm can eliminate or diminish noise in the wavelet coefficients while safeguarding or enhancing the essential signal component ⁴⁷. This contributes to improved signal quality, reduces noise interference, and simplifies the process of analyzing and interpreting the signal through subsequent processing techniques. The WT algorithm requires relatively minimal computational resources, allowing for prompt completion of processing, making it well-suited for real-time or large-scale data processing activities. Additionally, its implementation is uncomplicated as its underlying principles are relatively straightforward and do not necessitate an intricate mathematical background.

Threshold processing comprises two critical components: threshold selection and threshold function choice. Commonly utilized thresholds include the Sqtwolog, Rigrsure, Heursure, and Minimaxi thresholds ⁷.

The Sqtwolog threshold is implemented with minimal computational requirements, but may compromise its stability if the signal-to-noise ratio is low. Conversely, the Heursure threshold is stable, yet involves significant computational demands and necessitates iterative calculations. The Minimaxi threshold is grounded in solid theoretical principles and demonstrates stable performance; however, it requires considerable computational effort and its noise denoising effectiveness is moderate. The current study employs the unbiased risk estimation threshold, selected due to its reasonable computational demands when compared to the alternative thresholds. Furthermore, this threshold is chosen to optimize the preservation of valid signals characterized by small modal values.

Another crucial factor in WT denoising pertains to the selection of the threshold function. The hard and soft threshold functions emerge as the primary options.

The soft threshold function can be expressed as:

The hard threshold function can be expressed as:

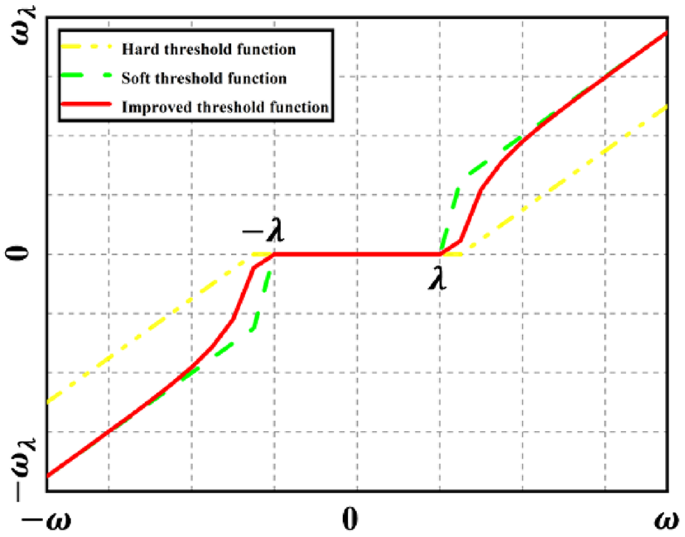
The hard threshold function exhibits discontinuities at thresholds (lambda ) and (-lambda ). Consequently, the wavelet inverse transformation generates a pseudo-Gibbs phenomenon, resulting in local signal oscillations that adversely affect reconstruction quality. Conversely, the soft threshold function maintains continuity at thresholds (lambda ) and (-lambda ), producing smoother signal waveforms. However, when (left|{omega }_{j,k}right|ge lambda ), ({widehat{omega }}_{j,k}) consistently diverges from ({omega }_{j,k}) by (lambda ). This introduces an intrinsic bias between the reconstructed signal and the original signal, leading to distortion in the reconstructed output.

While the conventional threshold function provides certain advantages, inherent drawbacks exist that influence noise reduction. To address the limitations of both the soft and hard threshold functions in noise reduction, the research proposes an innovative threshold function as follows:

In this equation, (mu =frac{lambda }{left|{omega }_{j,k}right|bullet textual content{exp}(left|frac{{omega }_{j,k}}{lambda }right|-1)}); ({omega }_{j,k}) signifies the wavelet coefficient; sgn(*) denotes the sign function; and (lambda ) represents the threshold value.

(1) Continuity assessment.

When ({omega }_{j,k}=lambda ), the left limit of ({widehat{omega }}_{j,k}) at (lambda ) is:

The precise limit of ({widehat{omega }}_{j,k}) at (lambda ) is:

When (left|{omega }_{j,k}right|=uplambda ), (mu =1, {widehat{omega }}_{j,k}(uplambda )=0). The enhanced threshold function maintains stability.

(2) Asymptotic analysis.

As (left|{omega }_{j,k}right|) increases, the construct (textual content{F}={widehat{omega }}_{j,k}-{omega }_{j,k}), which simplifies to:

As ({omega }_{j,kto infty ), (textual content{F}to 0), indicating that ({widehat{omega }}_{j,k}) steadily converges to ({omega }_{j,k}) as ({omega }_{j,k}) increases. By replacing ({omega }_{j,k}) with x and differentiating F(x), we obtain ({F}{prime}left(xright)>0), signifying that F(x) is monotonically increasing. The enhanced function preserves continuity at the threshold (lambda ).

influenced by the candidate cell state based on the results of the input gate.

As the parameter (mu ) nears 0 or 1, the enhanced threshold function consistently converges towards the traditional threshold function, ultimately synchronizing with it.

Figure 1 depicts the curves of the new, hard, and soft threshold functions. The new threshold function presents two significant advantages: it resolves the constant deviation issue found in the soft threshold function and alleviates the intermittency problem present in the hard threshold function.

Convolutional Neural Network

A convolutional neural network (CNN) serves as a mathematical model that emphasizes performing linear discrete convolutional operations. It boasts excellent feature learning capabilities and demonstrates remarkable robustness and fault tolerance. Its efficacy remains intact in the presence of translation, scaling, and distortion transformations ⁴⁸. Figure 2 showcases a typical CNN architecture.

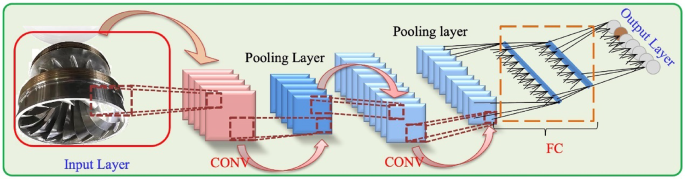
Standard structure of the CNN.

The CONV acts as the primary component of the CNN, carrying out convolutional tasks on input data and transmitting the output to subsequent layers of the network. Within the CONV layer, a convolutional kernel functions as the receptive field, moving across the entire input dataset with a defined stride.

Typically, activation functions are utilized to extract the nonlinear attributes inherent in the output data to enhance the model’s expressive capability. Activation functions are divided into saturated and unsaturated nonlinear functions. Compared to saturated nonlinear functions, employing unsaturated nonlinear functions assists in mitigating the issues of gradient explosion and gradient vanishing, thereby accelerating the model’s convergence. The Rectified Linear Unit (ReLU) stands out as a widely used unsaturated nonlinear activation function in CNN architectures. Its advantages, such as rapid convergence and straightforward gradient computation, significantly contribute to its popularity and appeal within the field.

To ensure the extraction of a sufficient variety of feature vectors, the output size of the convolutional layer is generally significant. However, a lower dimensionality may lead to overfitting issues. Integrating a pooling layer into the model efficiently reduces the number of parameters and aids in alleviating overfitting while preserving crucial characteristics of the output data. Common pooling techniques include average pooling and max pooling. The max pooling layer is advantageous for maintaining key features ⁴⁹, thus this research employs it as a pooling technique.

The fully connected layer acts as the final classification module in the CNN architecture, responsible for applying nonlinear activation to the extracted features and producing the probability distribution for each class. In this layer, every neuron connects to all neurons in the prior layer, establishing a mapping relationship between input features and output classes through learned weights and biases. The output of the fully connected layer undergoes an activation function, resulting in the probability distribution of the classification outputs. Consequently, the model can make precise classification predictions for input samples.

Long Short-Term Memory

The comprehensive structure of the LSTM network, illustrated in Fig. 3, comprises five main components: the unit state, hidden state, input gate, forgetting gate, and output gate. A distinctive characteristic of LSTM is the inclusion of three gating structures: an input gate, an output gate, and a forget gate. The architectural integration of gating mechanisms within LSTM networks provides a greater degree of control over the acceptance, retention, and dissemination of information ⁵⁰. This trait makes LSTM networks particularly adept at handling time series classification tasks.

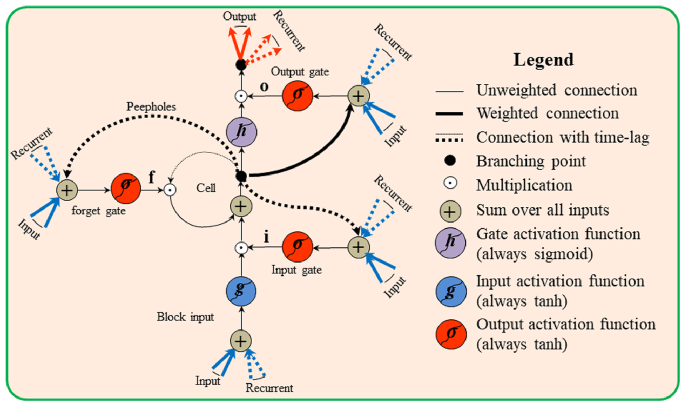
The state from the previous moment is retained within the state of the current LSTM unit, regulated by the forgetting gate. This gate serves as a mechanism to sift through the memory content, determining which information to preserve and which to discard. The LSTM is capable of effectively managing and updating its internal state by computing the forgetting gate. Its computation is expressed as follows:

In the above, ({{varvec{W}}}_{xf}) represents the weight matrix between the current input and the forgetting gate, (sigma ) indicates the chosen activation function, specifically the Sigmoid function with output bounded between 0 and 1, used to signal the extent of the gate’s openness, ({{varvec{f}}}_{t}) denotes the output of the forgetting gate, ({{varvec{h}}}_{t-1}) refers to the output state from the previous moment, ({{varvec{x}}}_{t}) stands for the current input state, ({{varvec{b}}}_{f}) signifies the bias term of the forgetting gate, and ({{varvec{W}}}_{hf}) is recognized as the weight matrix linking the historical output to the forgetting gate.

The input gate refreshes the state of the LSTM cell, determining if new input data should be stored. This gating structure produces an output value scaled between 0 and 1 by delivering the previous time step’s state and the current input data to an activation function. This output value quantifies the extent of the data that has been updated. A value close to 0 suggests that the input data is insignificant, whereas a value nearer to 1 implies that the input data is critical.

At the same time, the tanh function processes the previous state and current input information, scaling them to the range of -1 to 1 to yield the candidate cell state. As a result, the LSTM’s internal state can be influenced by the candidate cell state depending on the results from the input gate.

up to date, utilizing the input gate outputs and candidate cell states. This mechanism enables the LSTM community to effectively manage the reception and integration of recent information, aiding in modeling and analyzing sequential data. The output is then computed primarily based on this processed data:

In this equation, ({{varvec{i}}}_{t}) represents the input gate output, ({{varvec{W}}}_{hello}) is the weight matrix linking the previous output and the input gate, ({{varvec{W}}}_{xi}) is the weight matrix connecting the input and the input gate, and ({{varvec{b}}}_{i}) represents the bias term associated with the input gate.

The candidate cell state is defined as:

In this equation, ({{varvec{W}}}_{xc}) denotes the weight matrix between the input and cell state, ({widehat{{varvec{c}}}}_{t}) refers to the candidate cell state, ({{varvec{b}}}_{c}) signifies the bias term for the cell state, wherein the utilization of the hyperbolic tangent (tanh) function allows for scaling of the value, and ({{varvec{W}}}_{hc}) is the weight matrix linking the previous output to the cell state.

Using the outputs from both the forgetting gate and the input gate, the present LSTM cell state ({{varvec{C}}}_{t}) is determined by combining two components. The forgetting gate multiplies the prior cell state to ascertain the retained data, allowing it to selectively manage the forgetting of specific information from the previous state. Furthermore, the output of the input gate is multiplied by the current candidate cell state, indicating the portion of the data to be included. The input gate can regulate how much the newly received data influences the current state. The updated LSTM unit state ({{varvec{C}}}_{t}) is acquired by summing these two components. The LSTM accomplishes selective memory and data addition through its gating mechanisms. The cell state is expressed as:

The final output of the control unit state depends on the output gate. The current unit state data is multiplied by the output of the output gate. The tanh function is applied to the result to obtain the output value of the unit. The formula for the output gate can be expressed as:

In this expression, ({{varvec{W}}}_{ho}) is the weight matrix between the prior output and output gates, ({{varvec{W}}}_{xo}) is the weight matrix connecting the input and output gates, and ({{varvec{b}}}_{o}) represents the bias term for the output gate.

The formula for the unit output state is:

Wear fault diagnosis model of the CNN-LSTM

CNN and LSTM represent different feature extraction methods, each possessing unique characteristics. CNN is specifically designed to effectively capture spatially correlated features through convolutional filters, which is suitable for processing image and spatial data. In contrast, LSTM combines memory cells and gating mechanisms, primarily utilized to capture temporal correlations, making it appropriate for processing time-series data, such as natural language text or sensor data. However, CNNs exhibit certain limitations when addressing the temporal correlations of input variables. Conversely, LSTMs can learn and capture dependencies between previous and subsequent time steps in sequential data, leading to improved processing of temporal correlation features.

This study proposes a hybrid CNN-LSTM model for diagnosing wear faults in hydro-turbines. This model merges both CNN and LSTM architectures. This combination harnesses LSTM’s powerful temporal feature-capturing capabilities. The goal is to address the limitations of CNN when it comes to the temporal correlations of input variables. The proposed model can thoroughly analyze the input data via this integrative approach. Capturing both spatial and temporal correlation features enhances the reliability and accuracy of hydro-turbine fault diagnosis systems.

Within the CNN-LSTM fault diagnosis model, CNN assumes the role of extracting spatial features from the input data while reducing its dimensionality. On the other hand, LSTM uncovers latent temporal features within the data, utilizing its inherent long-term memory property to enhance data classification processes. The comprehensive model is illustrated in Fig. 4. Through a synergistic integration of CNN and LSTM, the model can effectively leverage their respective strengths, thereby supporting the diagnosis of wear faults in hydro-turbines. The initial stages of the diagnostic process consist of:

1. 1.

   Acquire the acoustic vibration signals associated with wear faults in hydro-turbines, categorize and segment the signals, compiling a standardized dataset of segmented data samples;

2. 2.

   The processed dataset is input into the CONV, where fault features are dynamically extracted using a convolutional filter;

3. 3.

   Following the CONV, the extracted features undergo max pooling to reduce the feature set’s dimensionality;

4. 4.

   The feature data, post-dimensionality reduction, will serve as input for training the neural network within the LSTM layer, enabling automatic learning of fault characteristics;

5. 5.

   Classification of features related to hydro-turbine faults utilizing Softmax functions.

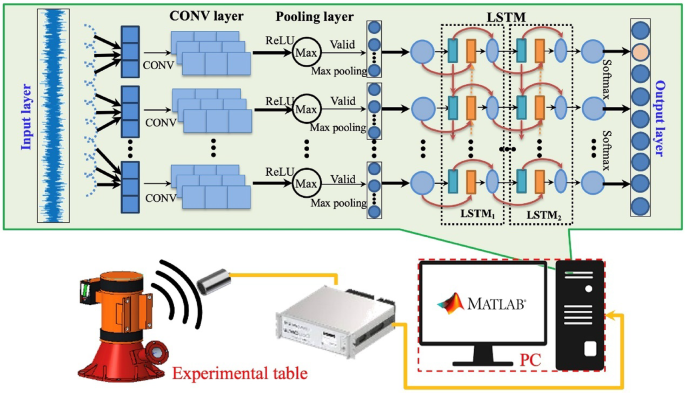
The steps outlined above describe the fundamental methodology of CNN-LSTM modeling for fault diagnosis in hydro-turbines. By fully utilizing the strengths inherent in CNN and LSTM, along with their complementary capabilities for spatial and temporal feature extraction, acoustic vibration signals undergo feature extraction processes followed by fault classification.