Harnessing the Power of Nature: How Hydroclimate Trends Shape Hydropower Production and Management

The primary objective of this investigation is to assess if and how hydroclimatic factors with biennial cycles can improve long-term hydropower generation (over timeframes of 3 and 6 months). To achieve this, the analysis utilizes a variety of methods, including stochastic forecasting, forecast accuracy evaluation, hydropower production simulations, an impact assessment framework, Monte Carlo simulations, and the formulation of biennial forecasting scenarios.

Stochastic hydrologic processes for forecasting

Various techniques in stochastic hydrology can be employed to model the unpredictable processes inherent in hydrology, such as the interplay between erratic and systematic climate changes^17,18 examined in this analysis. Information regarding hydrologic stochastic phenomena can be derived from historical records and presented as segmented time-series samples, which are then utilized in forecasting¹⁹. In this analysis, data from wet and dry years are segmented, and specific portions are randomly selected for forecasting.

The justification for employing hydrologic stochastic processes, based on the random extraction of time series segments, instead of a forecasting model (such as Global Climate Models) is threefold: (a) Natural systems are inherently intricate, nonlinear, and stochastic. Predictions based on observed time series are often more precise and reliable as the historical data samples are likely to recur in the future just as the original observations do; (b) forecasting models for short durations—such as hourly or daily time series—are too intricate to thoroughly capture all information present in historical observations. Stochastic processes, by extracting time series segments from historical data, maintain the complete spectrum of information, including extreme values that are challenging to replicate using traditional models; (c) model parameters can be influenced by trends and shifts within the observed data, thereby diminishing the dependability of those models²⁰; conversely, the stochastic process method preserves the integrity of the observed time series, making it less susceptible to inaccuracies introduced by data irregularities.

Stochastic forecasting employs historical record samples that are likely to demonstrate similar statistical characteristics in the future. Through the application of Monte Carlo sampling, a sufficiently large number of forecasted samples is generated, facilitating the creation of frequency distributions of various time-series metrics, such as mean and variance, along with auto-covariation across different frequencies²⁰. These metrics are often challenging to compute through alternative methods for generating stochastic time series.

Let (:{xi:}_{T}ge:0) denote the historical runoff time series for the entire dataset time horizon, T. (:{t}_{0}) represents the moment at which historical runoff data commence. An arbitrary sequence of times (:{t}_{i}) is selected between (:{t}_{0}) and T, where i is the index for the selected time. A set of randomly generated runoff values with n samples for a forecasting horizon (:{T}_{H}) can be represented as (:left{{xi:}_{{t}_{i}},:{xi:}_{{t}_{i}+1},:{xi:}_{{t}_{i}+2},dots:,:{xi:}_{{t}_{i}+{T}_{H}-1}proper}), where index i = 1, 2, 3,…, n.

Based on the biennial cycle in runoff, two classifications of runoff data can be extracted from the historical time series. One comprises the data from wet years (:{xi:}_{T}^{moist}), and the other the data from dry years (:{xi:}_{T}^{dry}), reflecting the biennial hydroclimate pattern. For the stochastic forecasting of a wet year, this can be expressed as (:left{{xi:}_{{t}_{i}}^{moist},:{xi:}_{{t}_{i}+1}^{moist},:{xi:}_{{t}_{i}+2}^{moist},dots:{,xi:}_{{t}_{i}+{T}_{H}-1}^{moist}:proper}), where index i = 1, 2, 3,…, n, and (:{t}_{i}) is exclusively chosen from wet years. Conversely, the forecasting of runoff for a dry year is (:left{{xi:}_{{t}_{i}}^{dry},:{xi:}_{{t}_{i}+1}^{dry},:{xi:}_{{t}_{i}+2}^{dry},dots:{,xi:}_{{t}_{i}+{T}_{H}-1}^{dry}:proper}), where index i = 1, 2, 3,…, n, with (:{t}_{i}) being chosen solely from dry years. Furthermore, a question arises: to what extent does the commencement month of the biennial cycle affect the effectiveness of hydropower management? To explore this issue, this study examines the commencement months of the biennial cycle for the forecasting samples employed in stochastic forecasting. For instance, one set of forecasting samples for a wet year beginning in January may be (:left{{xi:}_{{t}_{i}}^{moist,Jan},:{xi:}_{{t}_{i}+1}^{moist,Jan},:{xi:}_{{t}_{i}+2}^{moist,Jan},dots:{,xi:}_{{t}_{i}+{T}_{H}-1}^{moist,Jan}:proper}), where index i = 1, 2, 3,…, n, and (:{t}_{i}) is specifically selected from wet years in January.

Performance evaluation

The effectiveness of the forecasting model is assessed based on its precision, which is determined by the discrepancies between forecasted samples and the actual observed data. Since actual future information cannot be directly observed, a simulated “actual” trend is created to represent anticipated observations. In this investigation, the actual trend is characterized by the mean value of runoff data selected from classifications similar to the scenarios.

The divergence between the predicted samples and the simulated actual data is measured using the Nash-Sutcliffe efficiency coefficient (NSE), as delineated in Eq. 1. NSE is widely used to assess the predictive capability of hydrological models, with values ranging from –∞ to 1, where NSE = 1 corresponds to a perfect agreement between the forecasts and the observed data^21,22,23. An efficiency of 0 (NSE = 0) indicates that the model predictions are as precise as the average of the observed data, while an efficiency below zero (NSE lt; 0) implies that the residual variance exceeds the variance of the data.

However, the lower limit of NSE at negative infinity can complicate its interpretation and representation. To mitigate this issue, the normalized Nash-Sutcliffe efficiency (NNSE) is utilized to rescale the NSE, as defined in Eq. 2. In this formulation, NNSE = 1 corresponds to NSE = 1, NNSE = 0.5 corresponds to NSE = 0, and NNSE = 0 signifies NSE < –(:infty:). This rescaling simplifies the evaluation of the model’s performance.

Where, j is the index of forecasting values, and J is the total number of forecasting values in a single sample. (:{q}_{r})stands for the simulated actual runoff, while (:{q}_{f}) denotes the predicted runoff.

Energy production efficiency ((:eta:)) is defined as the potential production divided by the difference between potential runoff energy and potential storage energy, as demonstrated in Eq. 3. The potential production ((:{E}_{pd})) is the simulated downstream production, representing the estimated output generated at each station plus the potential production from all downstream stations along the water course towards the ocean. The potential runoff energy ((:{E}_{rd})) and potential storage energy ((:{E}_{sd})) account for the total downstream energy and not just for the individual station.

Hydropower operation model

The hydropower operation model developed using MATLAB R2022b for this research employs a step-linear optimization approach, crafted to enhance the planning and production of cascade hydropower plants and reservoirs. In practice, planning equates to solving an optimization problem, where the objective must conform to specific constraints. The aim of the hydropower optimization model is to maximize electricity generation while maintaining the highest feasible water levels in the reservoirs. This objective is mathematically illustrated by the maximization of the target function F, as defined in Eq. (4).

Where (:{T}_{H})(days) represents the optimization time horizon (equivalent to the forecasting horizon), (:{left({E}_{p}proper)}_{{T}_{H}})(J) signifies the energy generated by hydropower throughout the complete optimization time horizon (:{T}_{H}) (days), which can be calculated using Eq. (5). (:{left({E}_{w}proper)}_{{T}_{H}})(J) indicates the potential water energy stored in reservoirs for the duration (:{T}_{H}) (days) and can be harnessed to generate electricity in the future. (:{left({E}_{w}proper)}_{1}) represents the initial potential water energy. The potential water energy is computed as a function of the downstream elevation (:{h}_{f}) (m), as per Eq. (6), incorporating the water elevation from the station to sea level along with the downstream stations. (:{left({E}_{w}proper)}_{1}:) is the initial potential water energy (Eq. (7)), which pertains to the energy stored in reservoirs at the outset of the hydropower optimum operation.

ρ (kg/m³) denotes the density of water; g (m/s²) represents the acceleration due to gravity; and η is the fixed generation efficiency of a hydropower facility; h (m) refers to the water level in a station; q (m³/s) symbolizes the turbine discharge; (:{Delta:}t) describes the time interval of energy production. A (m²) signifies the surface water area of each reservoir.

The constraints of the hydropower optimization model encompass water conservation, which delineates the dynamic water flows within the river basin between each hydropower station, alongside the limitations of variables such as turbine discharge and water head. These constraints are articulated in Eq. (8)

Where (:{V}_{t}) signifies the volume of water within the reservoir at time index t. (:{q}_{up,t}) and (:{s}_{up,t}) represent the turbine discharge and spill discharge from the upstream station at time index t. The stations are interconnected by river channels and, as such, receive water flow from the discharge of the upstream stations. The water from upstream stations can be utilized to generate electricity multiple times while passing through several hydropower facilities. (:{q}_{t}) and (:{s}_{t}) indicate the turbine and spill discharges at the current station at time index t. (:underset{_}{h},:overline{h}) and (:underset{_}{s},:overline{s}) are the upper and lower limits of water level and spill discharge. (:overline{q}) designates the maximum limit of turbine discharge. The transit time of water flow between stations is disregarded, and the river channel is simplified as rectangular.

Model for evaluating hydroclimatic periodic impacts

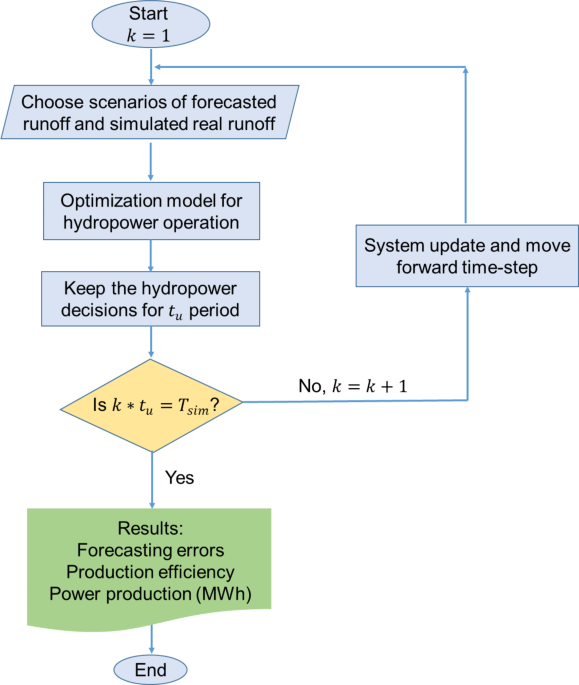
To assess the effects of hydroclimatic periodic runoff on hydropower production and management, this study utilizes an analytical model constructed to simulate the management efficiency of hydropower generation. This model accounts for the uncertainty associated with water availability forecasts and reflects the long-term periodicity observed in hydroclimatic time series. This analytical model, designed by Hao et al. 2023, consists of two main submodels: (a) an optimization model that optimizes hydropower operations by considering forecasted future runoff for J future scenarios along a time horizon (:{T}_{H}), water conservation within the river basin, and energy generation; and (b) a system update step, a submodule that refreshes the system after a shorter interval (:{t}_{u}). The optimal production decisions are applied during the updating interval(:{t}_{u}) for each simulation across the (:{T}_{H}) horizon based on the receding horizon approach and the shifting horizon of various stochastic runoff forecasts over the time series, spanning a simulation period, (:{T}_{sim}) ultimately. The update incorporates the actual runoff and reservoir levels, aiming to ensure that the impacts of forecasting errors do not compound over time, thereby accurately representing the true operational planning process over a more detailed timeframe.

prolonged duration. To provide a selection pathway that is statistically representative, the optimization is executed N times for each (:{t}_{u}) interval with varying stochastic projected runoff. Consequently, the average values of these N optimal selections of generation and discharge spills are utilized as determined values for an updating time interval, (:{t}_{u}).

The streamlined model architecture is depicted in Fig. 1. The inputs comprise the predicted runoff scenarios and the simulated actual runoff conditions for the time horizon (:{T}_{H}), produced utilizing methods outlined in Sect. 2.1. Monte Carlo simulation is employed for runoff forecasting during the simulation span, (::{T}_{sim}), while the simulated actual runoff is assumed to be a fixed time-series of runoff for each scenario. The outputs represent the forecasting errors of the runoff, which denote the difference between predicted samples and actual samples of runoff, the generation efficiency from the simulation of the hydropower optimal operation model, and the power output. The model parameters can be found in the supplementary information Table S1.

Monte Carlo simulation

Monte Carlo (MC) simulation enables the characterization of a distribution without the necessity of understanding its mathematical attributes, by randomly sampling values from the distribution^24,25. In this research, the effect of climate periodicity on hydropower management has been analyzed through stochastic forecasting. A singular random forecast is inadequate to capture the complete picture of the effect. Thus, MC simulation is employed to examine a range of potential outcomes.

While MC simulation is beneficial for its straightforward implementation with complex models, it demands considerable computational resources to produce reliable results^24,26. To enhance the efficiency of the MC simulation of the assessment model, we conducted tests to identify the optimal number of MC iterations. Specifically, we evaluated the Control-Control scenario with January as the initiating month, using a three-month simulation period, and varying the number of MC runs from 20 to 300. Refer to Sect. 2.6 for comprehensive information. The variance, standard deviation, and mean of production efficiency are summarized in Table 1. The data indicates that the variance, standard deviation, and mean values stabilize with 100 MC simulations. Therefore, 100 MC iterations are considered optimal for balancing result reliability and computational efficiency. As a result, all subsequent MC simulations in this research are executed 100 times for each forecasting scenario.

Hydroclimate biennial conditions

The hydroclimate conditions exhibiting biennial periodicity implemented in this research are based on the hydrologic stochastic forecasting technique described in Sect. 2.1. This approach aims to segregate the biennial periodicity within the runoff during dry and wet years. The predicted runoff statistically deviates from the utilized actual runoff scenario. It has been observed that odd years are generally wetter than the average year, whereas even years tend to be drier for the Dalälven River Basin⁵. The historical data of runoff can thus be segmented into three categories based on the biennial periodicity: Classification 1 contains the wet-year data; Classification 2 comprises the dry-year data; Classification 3 serves as a control group data, including all years regardless of whether they are odd or even.

The seven scenarios presented in Table 2 are developed based on these three classifications.